Welcome to our guide on Exponent Rules. Here, we'll break down the essentials of working with powers, making math straightforward and accessible. Let's dive into the world of exponents together!
| Rule name | Rule | Example |
|---|---|---|
| Product rules | a n ⋅ a m = a n+m | 2 3 ⋅ 2 4 = 2 3+4 = 128 |
| a n ⋅ b n = ( a ⋅ b) n | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| Quotient rules | a n / a m = a n - m | 2 5 / 2 3 = 2 5-3 = 4 |
| a n / b n = ( a / b) n | 4 3 / 2 3 = (4/2) 3 = 8 | |
| Power rules | ( b n ) m = b n⋅m | (2 3) 2 = 2 3⋅2 = 64 |
| b n m = b( n m ) | 2 3 2 = 2( 3 2 ) = 512 | |
| m √( b n ) = b n/ m | 2√(2 6) = 2 6/2 = 8 | |
| b 1/ n = n √ b | 8 1/3 = 3√ 8 = 2 | |
| Negative exponents | b -n = 1 / b n | 2 -3 = 1/2 3 = 0.125 |
| Zero rules | b 0 = 1 | 5 0 = 1 |
| 0 n = 0 , for n>0 | 0 5 = 0 | |
| One rules | b 1 = b | 5 1 = 5 |
| 1 n = 1 | 1 5 = 1 | |
| Minus one rule |
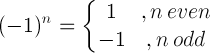
|
(-1) 5 = -1 |
| Derivative rule | ( x n ) ' = n⋅ x n -1 | ( x 3) ' = 3⋅ x 3-1 |
| Integral rule | ∫ x ndx = x n +1/( n+1)+ C | ∫ x 2 dx = x 2+1/(2+1)+ C |
Defining Exponents: An exponent showcases how many times a number, termed as the base, is multiplied by itself.
Exponent Formula: When a number 'a' is raised to the power 'n', it means 'a' is multiplied by itself 'n' times:
a^n = a × a × ... (up to n times)
Here, 'a' is our base while 'n' stands as the exponent.
Illustrative Examples:
Exponent Calculator: For those seeking a quicker solution, an exponent calculator can automate these multiplications, providing swift and accurate results.
By grasping these principles and examples, the realm of exponents becomes more accessible and less daunting.
Multiplying Exponents with the Same Base: When bases are identical but exponents differ: a^n ⋅ a^m = a^(n+m)
Illustration: 2^3 ⋅ 2^4 = 2^(3+4) = 2^7 = 128
Multiplying Exponents with the Same Power: When exponents are identical but bases differ: a^n ⋅ b^n = (a⋅b)^n
Illustration: 3^2 ⋅ 4^2 = (3⋅4)^2 = 144
For more, refer to:
Dividing Exponents with the Same Base: With identical bases: a^n / a^m = a^(n-m)
Illustration: 2^5 / 2^3 = 2^(5-3) = 4
Dividing Exponents with the Same Power: With identical powers: a^n / b^n = (a/b)^n
Illustration: 4^3 / 2^3 = (4/2)^3 = 8
Explore further:
Exponentiation of Exponents - Rule I: (a^n)^m = a^(n⋅m)
Illustration: (2^3)^2 = 2^(3⋅2) = 64
Exponentiation of Exponents - Rule II: a^(n^m) = a^(n⋅m)
Illustration: 2^(3^2) = 2^(3⋅3) = 512
Radical Power Rule: m-th root of a^n = a^(n/m)
Illustration: Square root of 2^6 = 2^(6/2) = 8
Dealing with Negative Exponents: b^-n = 1/b^n
Illustration: 2^-3 = 1/2^3 = 0.125
By understanding these exponent rules, mathematical operations involving powers become far more intuitive and manageable.
Understanding exponent rules is crucial as they form the foundation for many mathematical and algebraic operations. Grasping these rules ensures accuracy when working with powers and simplifies complex calculations, making problem-solving more efficient.